Strukturanalyse

Im täglichen Leben trifft man auf viele verschiedene Arten von dünnen flüssigen Filmen, z.B. bei Schmiermitteln, Farben oder Polymerfilmen. Sind solche Filme instabil, kommt es zur Entnetzung. Es bilden sich Löcher, die anwachsen und zunehmend die Oberfläche dominieren, bis schließlich nur isolierte Flüssigkeitstropfen zurückbleiben. Es gibt mehrere Mechanismen, die zur Lochbildung in dünnen Filmen führen, z.B. die Anwesenheit von Fremdkörpern und intrinsischen Spannungen. Außerdem können thermische Fluktuationen der Filmoberfläche zu Oberflächenwellen führen, deren Amplitude die Größenordnung der Filmdicke erreichen kann, was ebenfalls zur Lochbildung führt (spinodales Entnetzen). Ein Thema dieser Forschungsrichtung beinhaltet die experimentelle Quantifizierung von Entnetzungsstrukturen mit Rasterkraft- und optischer Mikroskopie. Dadurch soll der sog. Slip an der Grenzfäche zwischen fester und flüssiger Phase charakterisiert werden, um bessere Näherungen für die theoretische Vorhersagbarkeit solcher Entnetzungssysteme angeben zu können.

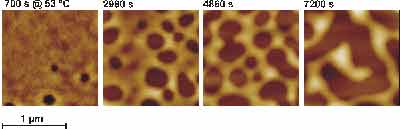
Abb.1 : Zeitlicher Verlauf einer Entnetzung

Die räumlichen Strukturen, die bei solchen Entnetzungsprozessen entstehen, sind unsymmetrisch und ungeordnet, was die Beschreibung schwierig macht. Übliche Analysemethoden wie die Paarkorrelationsfunktion und die Fouriertransformation können für diese komplexen Systeme nicht angewendet werden, weil sie nur die Zwei-Punkt-Korrelationen und damit eine Verteilung von Abständen darstellen können. Im Gegensatz dazu findet man in der Integralgeometrie einen Satz von geeigneten morphologischen Maßen, die sog. Minkowski - Funktionale. Mit ihnen kann nicht nur die Topologie (Verbundenheit), sondern auch die Geometrie (Flächeninhalt und Form) von räumlichen Mustern charakterisiert werden. Ein weiterer Aspekt der Forschung ist es also, einen geeigneten Algorithmus zu finden, um diese Funktionale zu berechnen und damit reale, komplexe Oberflächen beschreiben zu können.