Strukturbildung und Dynamik in makromolekularen Filmen
(aus: Nachrichten aus der Chemie 49 (2001) 1398-1404)
Wer die Mikro- und Nanotechnologie von morgen beherrschen will, muss Materialeigenschaften auf kleinster Skala charakterisieren und verstehen. Selbstorganisierte Strukturbildung in dünnen Filmen ist ein möglicher Weg dorthin, und ein ästhetischer obendrein.
Haben Sie schon einmal versucht, mit Wasserfarben auf einer Porzellan- oder Kunststoffoberfläche zu malen? Dann kennen Sie die charakteristischen Tropfenmuster, die entstehen, wenn ein flüssiger Film von einer Oberfläche abperlt, die er nicht benetzt. Dieses Abperlen (oder Entnetzen, wie es im Jargon heißt) ist im Allgemeinen unerwünscht, und wer es zuverlässig verhindern will, muss im Einzelnen verstehen, wie das Aufreissen und Abperlen eines flüssigen Filmes von einer festen Unterlage vor sich geht. Hat man diese Kenntnis einmal gewonnen, kann man aber vor allem aus den charakteristischen Entnetzungsstrukturen bzw. Tropfenmustern wertvolle Informationen über die dynamischen Eigenschaften und molekularen Wechselwirkungen der beteiligten Materialien gewinnen. Diesen Aspekt wollen wir uns hier herausgreifen, wobei wir besonderes Augenmerk auf makromolekulare Filme legen wollen, da diese von großem technologischem Interesse sind.
Es ist zunächst zu betonen, dass der Prozess der Entnetzung, der einen ursprünglich homogenen Film in eine Anordnung isolierter Tropfen überführt (siehe Abb. 1a), mehrere Stadien durchläuft, in denen jeweils unterschiedliche Strukturbildungsmechanismen in Konkurrenz treten. Um diese im Experiment klar und ohne Störeinflüsse zu beobachten, muss man zunächst einen sehr glatten Film auf ein Substrat aufbringen, das vom Filmmaterial nicht benetzt werden will, das also hydrophob ist. In unseren Experimenten wurde der Film zunächst auf eine Wasseroberfläche gebracht, wo er als stabiles Gebilde oben aufschwimmt. Von dort kann er ohne große Mühe auf eine hydrophobe Festkörperoberfläche übertragen werden (die er im flüssigen Zustand meiden würde). Hierbei handelt es sich um Siliziumwafer, die durch kovalente Anbindung von Alkylsilan-Monoschichten hydrophob gemacht wurden [1]. Erwärmt man die so präparierten Filme über ihre Schmelztemperatur, beginnt der Entnetzungsprozess, den man unter dem optischen Mikroskop beobachten kann. Ein typisches Tropfenmuster, das das Endstadium eines solchen Prozesses darstellt, ist in Abb. 1b gezeigt.
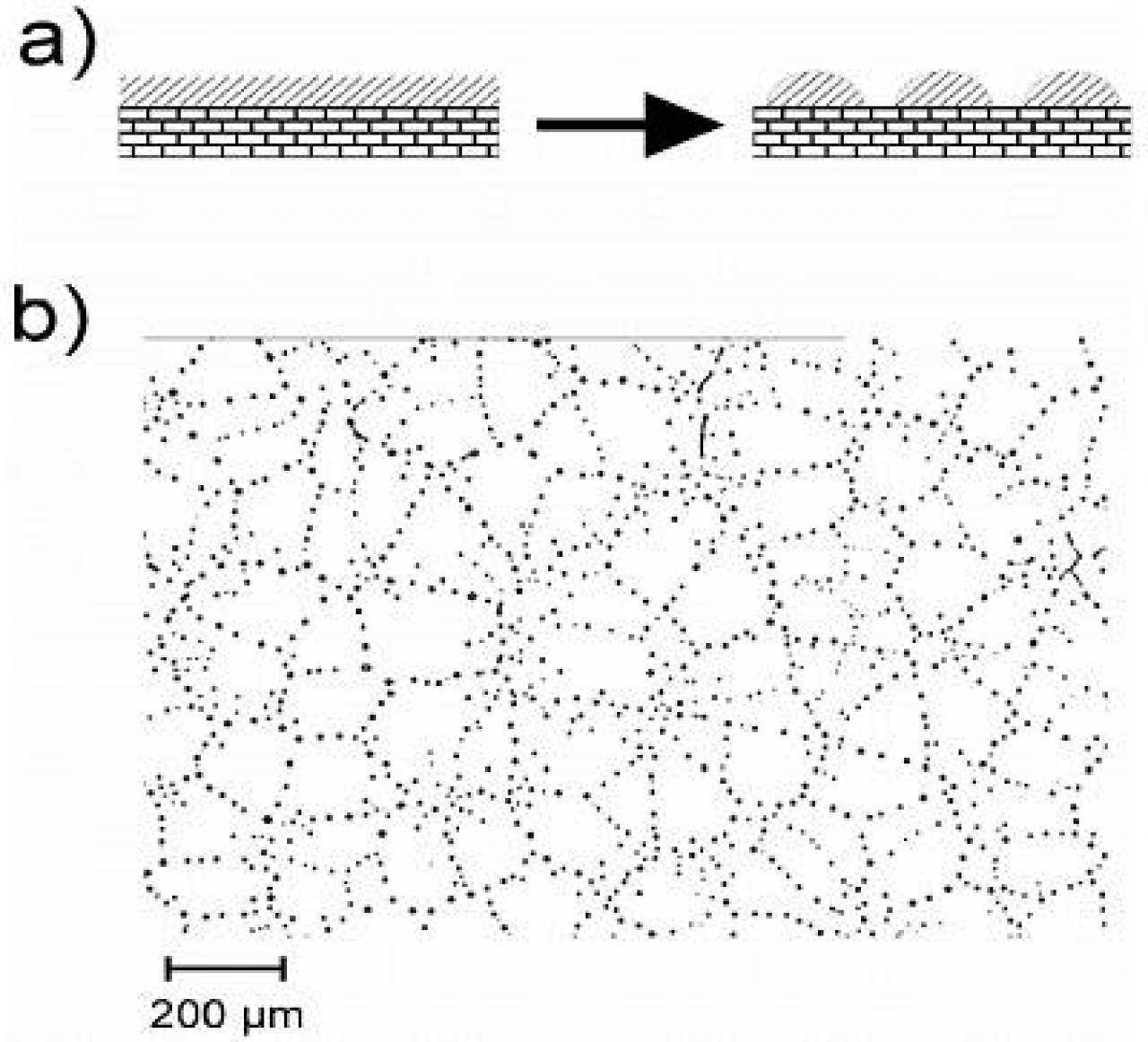
Abb. 1: a) Entnetzung in schematischer Darstellung: Ein zunächst homogener Film (schraffiert), der das Substrat nicht benetzen will, perlt ab und bildet einzelne Tropfen. b) Lichtmikroskopische Aufnahme des Endstadiums eines Entnetzungsprozesses. Die Tropfen bilden ein charakteristisches Muster, das Informationen über die Dynamik des Entnetzungsprozesses enthält.
Frühstadium der Entnetzung
Fragen wir nun zunächst nach dem Frühstadium der Entnetzung: was sind die ersten Anzeichen dafür, dass ein homogener Film auf einer glatten Unterlage zu entnetzen beginnt? Wenn wir wirklich von einem Film homogener Dicke starten, so müssen wir die Frage dahingehend präzisieren, wie die erste Auslenkung der freien Filmoberfläche zustande kommt. Zwar wird die Oberfläche durch thermische Fluktuationen ausgelenkt, jedoch liegt deren Amplitude meist nur im Angströmbereich, denn die Oberflächenspannung wirkt als starke Rückstellkraft. Da der Film stets viele Atomlagen dick ist, können diese Fluktuationen i. Allg. keine Entnetzung herbeiführen.
Es gibt aber eine wichtige Ausnahme: wenn die van der Waals-Wechselwirkung zwischen den Molekülen des Filmmaterials und denen des Substratmaterials schwächer ist als die der Filmmoleküle mit ihresgleichen, ergibt sich eine vortreibende Kraft für die Auslenkungen der Oberfläche, die der rückstellenden Wirkung der Oberflächenspannung entgegenwirkt [2]. In diesem Falle gibt es einen begrenzten Wellenlängenbereich, in dem die Amplitude der Fluktuationen exponentiell anwächst, sodass schließlich die Filmoberfläche das Substrat erreicht: Löcher entstehen im Film, Entnetzung setzt ein. Eine genauere Betrachtung zeigt, dass im Wesentlichen eine einzige Wellenlänge den Prozess dominiert, was man am Entnetzungsmuster auch deutlich sieht. In Abb. 2 ist dies für einen Flüssigkristallfilm gezeigt [2]. Aus der Wellenlänge und der charakteristischen Zeitskala, in der das Muster entsteht, kann man nun Größen wie die Viskosität des Filmmaterials und dessen van der Waals-Wechselwirkung mit dem Substrat berechnen [2, 3, 4].

Abb. 2: Entnetzungsmuster in einem etwa 40 nm dicken Film aus einem Flüssigkristall (5AB4, optische Mikroskopie in Reflexion). Deutlich zu erkennen ist das undulative Muster, das auf instabile Oberflächenwellen zurückzuführen ist.
Rheologie dünner Polymerfilme
Bei Polymeren ist nun gerade die Viskosität dünner Filme von großem aktuellen Interesse. Seit einiger Zeit weiß man nämlich, dass die Glastemperatur (und damit die Viskosität) in Filmen dünner als ca. 100 nm erheblich reduziert sein kann [5]. Bei großen Molekulargewichten ist dies durchaus nicht verwunderlich: bei 500 kg pro Mol beispielsweise ist ein Polystyrolmolekül schon fast einen Mikrometer lang, wenn man es ausstreckt. Sperrt man solche Objekte in einen Film mit einer Dicke von 100 nm oder weniger ein, so kann man einen Einfluss auf die Dynamik schon erwarten. Erstaunlicherweise stellt man aber fest, dass die Erniedrigung der Glastemperatur, zumindest für Molekulargewichte bis etwa 300 kg pro Mol, praktisch unabhängig vom Molekulargewicht ist [6], was mit dieser einfachen geometrischen Modellvorstellung nicht verträglich ist.
Um den Effekt noch klarer hervortreten zu lassen, haben wir den Extremfall untersucht: dünne Filme aus ataktischem Polystyrol mit einem Molekulargewicht von nur 2 kg pro Mol, das entspricht einem Gyrationsradius von nur etwa 1.3 nm. Über die Viskosität, die wir aus dem Entnetzungsverhalten erschließen konnten, ermittelten wir die Glastemperatur extrem dünner Filme (< 10 nm). Optische Dilatometrie lieferte uns die notwendigen Daten für größere Dicken (> 10 nm). Wie Abb. 3 zeigt, nimmt die Glastemperatur bereits bei Dicken von ca. 50 nm deutlich ab, um bei den dünnsten Filmen schließlich um über 50 K reduziert zu sein. Keine der bisher vorgestellten Theorien, die alle die Dynamik des Einzelmoleküls im Blick haben, kann diesen Effekt zufriedenstellend erklären.
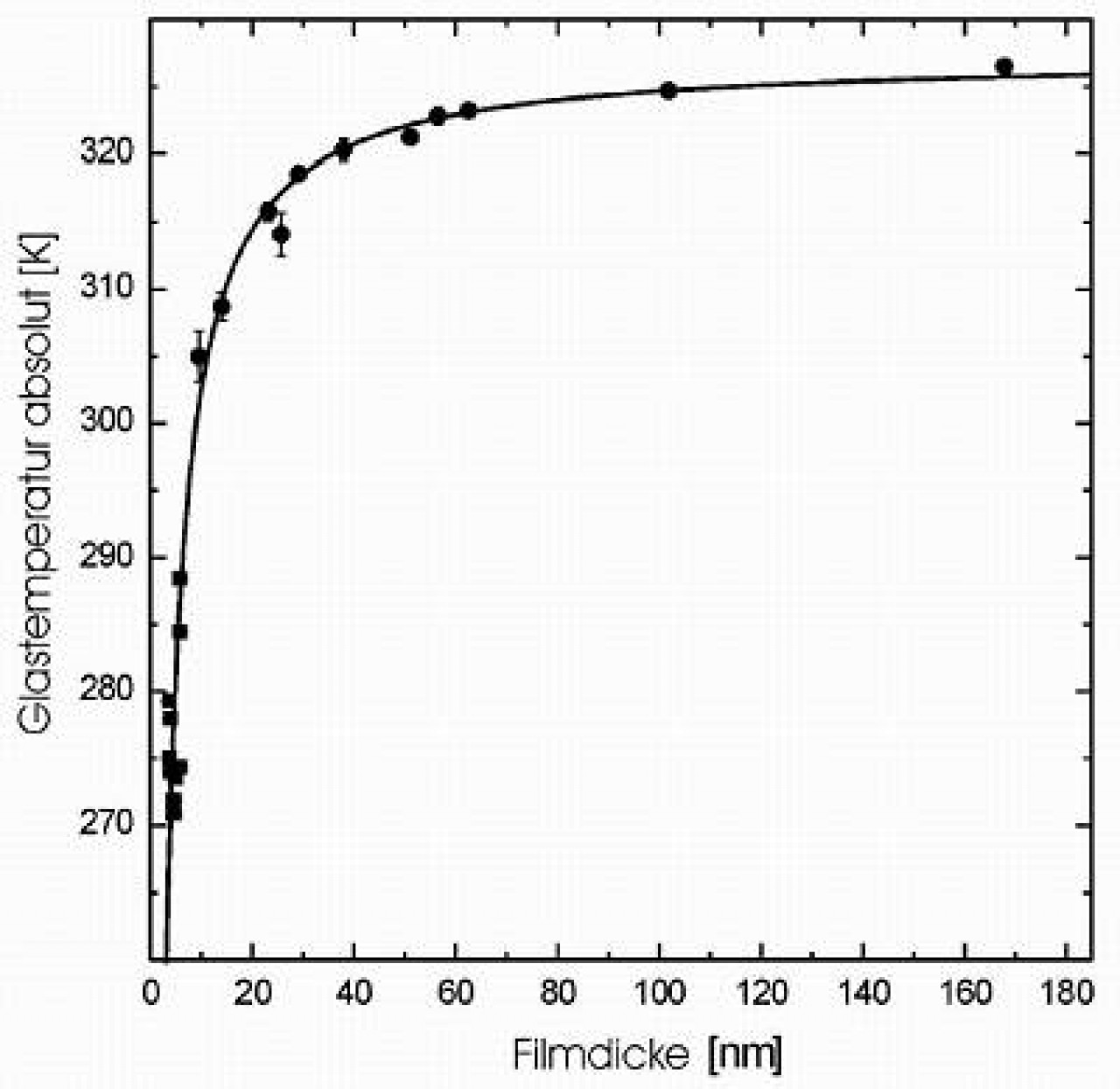
Abb. 3: Abhängigkeit der Glastemperatur dünner Polystyrolfilme von der Filmdicke. Die durchgezogene Kurve repräsentiert den nach unserer Theorie erwarteten Verlauf.
Welche kollektiven, geometrieabhängigen Einflüsse auf diese Dynamik sind nun denkbar? Die Kopplung der Konformationsfluktuationen einzelner Moleküle an die freie Filmoberfläche wird durch das Spektrum der viskoelastischen Eigenmoden des Films vollständig beschrieben. Wir haben festgestellt, dass dieses Spektrum in Kombination mit der für den Glasübergang bekannten Modenkopplungstheorie [7] einen Ausdruck ergibt, der die experimentellen Ergebnisse perfekt beschreibt. Er liefert die durchgezogene Linie, die sehr gut nicht nur an unsere, sondern auch an die Daten anderer Gruppen passt. Der einzige Anpaßparameter ist der elastische Schermodul des Polymeren nahe der Glastemperatur, für den eine gewisse Wahlfreiheit besteht, da er sich in diesem Temperaturbereich um mehrere Größenordnungen ändert. Der Erfolg dieses Modells legt die Vermutung nahe, dass die Erniedrigung der Glastemperatur im dünnen Film tatsächlich eine direkte Folge der Kopplung der Dynamik des Einzelmoleküls an die Deformationen der Filmoberfläche ist.
Warum zerstört ein Polymerfilm sich selbst?
Kehren wir zurück zu Abb. 2. Neben dem sehr gleichmäßgen Wellenmuster, das klar eine charakteristische Wellenlänge aufweist (ca. 10 µm), sieht man noch eine weitere, konkurrierende Struktur: einige mehr oder weniger kreisrunde Löcher sind entstanden, deren Ränder etwas erhöht erscheinen. Hier haben einzelne Nukleationskeime für die Entnetzung gesorgt; in diesem Falle wahrscheinlich Staubkörner, denn dieses Experiment wurde nicht in Reinraumatmosphäre durchgeführt. Ein Korn ist auch im Zentrum des zugehörigen Loches deutlich sichtbar (Pfeil).
Tatsächlich ist dieser Mechanismus der Nukleation sogar der Normalfall, und keineswegs auf Dreckeffekte beschränkt, wie wir im Folgenden zeigen wollen. Abb. 4 zeigt eine mikroskopische Aufnahme eines Polystyrolfilms, der zunächst im festen Zustand auf einen hydrophoben Siliziumwafer aufgebracht (s.o.) und dann über seine Glastemperatur erhitzt wurde. Ataktisches Polystyrol wurde gewählt wegen seiner Reinheit und der Abwesenheit jeglicher Kristallisationsneigung, was es als gut zugängliches Modellsystem ausweist. Wie man in der Abbildung sieht, vollzieht sich der Entnetzungsprozess hier ausschließlich durch die Entstehung einzelner, kreisrunder Löcher, wie wir sie bereits oben kennengelernt hatten. Die Lochanordnung weist keinerlei räumliche Korrelation auf, was zeigt, dass es sich hier um einen statistischen Prozess handelt, wie im Falle der Nukleation erwartet. Eine bevorzugte Längenskala, wie im Falle der instabilen Oberflächenwellen, ist nicht vorhanden [2, 8].

Es stellte sich heraus, dass die Nukleation von Löchern im Film auch durch noch so sauberes Arbeiten offenbar nicht vermieden werden kann. Vielmehr gibt es Hinweise, dass es sich nicht notwendigerweise um Fremdkeime (wie etwa Staubkörner) handelt, sondern dass eine Nukleation allein schon durch strukturelle Eigenschaften des Polymerfilms hervorgerufen wird. Vergegenwärtigen wir uns, dass die meisten Polymerbeschichtungen aus der Lösung heraus präpariert werden, ob durch Rakeln, Tauchen oder Schleudern. Auch die in unseren Experimenten verwendeten Filme wurden zunächst auf ein hydrophiles Substrat, nämlich frisch gespaltenen Glimmer, aus einer Toluol-Lösung aufgeschleudert, von dort auf die Wasseroberfläche (s.o.), dann auf den hydrophobisierten Siliziumwafer übertragen.
Eine generelle Eigenschaft aller aus Lösung präparierten Polymerfilme ist aber ihre innere Verspannung [9]. Man erzeugt ja zunächst einen homogenen Film aus Polymerlösung, aus dem das Lösemittel langsam abdampft, um schließlich den erstarrten Film aus reinem Polymeren zu hinterlassen. Dabei steigt die Glastemperatur des Films allmählich an, bis sie die des Poymeren erreicht hat (im Falle des Polystyrols sind das etwa 100°C). Sobald aber die Glastemperatur größer ist als Raumtemperatur, können sich die Moleküle nicht mehr rearrangieren. Während der Film nun bei weiterem Lösemittelverlust dünner wird, werden die Molekülknäuel vertikal zusammengedrückt, ohne lateral nachgeben zu können. Als Resultat sind sie im schließlich verfestigten Film etwas plattgedrückt, was einer Verspannung des Materials entspricht. Diese hängt nicht von der Filmdicke, sondern nur von der Wahl des Lösemittels ab und beträgt im Falle des Polystyrols bei Verwendung von Toluol (wie bei unseren Experimenten) etwa 14 MPa [9].
Hat diese generell vorhandene Verspannung nun einen Einfluss auf die Nukleation? Um dies zu prüfen, haben wir Polystyrolfilme, während sie noch auf dem Glimmer waren, unterschiedlich lange bei Temperaturen oberhalb der Glastemperatur getempert. Dadurch sollte die beim Präparationsprozess eingefrorene Verspannung teilweise ausgeheilt werden. Tatsächlich wird die Flächendichte der anschließend (nach Übertragung auf das hydrophobe Substrat) durch Nukleation entstehenden Löcher dadurch drastisch beeinflusst wird. Je länger der Film auf dem Glimmer vorgetempert wurde, desto weniger Löcher reißen je Quadratmillimeter auf. Wir sehen also, dass die intrinsische Verspannung allein schon für Entnetzung sorgt. Sauberes Arbeiten allein wird also niemals genügen, um dies zu verhindern!
Bleibt noch zu fragen, welche morphologischen Besonderheiten des Materials die Positionen der so entstehenden Löcher bestimmen. Einen Hinweis bekommt man, wenn man die Kettenlängenabhängigkeit dieses Effektes überprüft. Man findet, dass unterhalb der Verhakungslänge (bei Polystyrol etwa 15 kg pro Mol) keine Löcher mehr entstehen, was auf einen molekularen Ursprung der Lochentstehung weist. Die genauere Ursache ist bisher ungeklärt und wird zur Zeit intensiv untersucht.
Viskoelastische Effekte
Schaut man sich die Form der Löcher etwas genauer an, kann man eine Menge über die rheologischen Eigenschaften des Filmmaterials lernen. So zeigt Abb. 5a einen Querschnitt durch den Randwulst eines solchen Loches, wie er mir einem Rasterkraftmikroskop (AFM) aufgenommen wurde. Klar erkennt man auf der linken (Innen-) Seite denPunkt, an dem die Oberfläche das Substrat trifft. Rechts geht der Wulst stetig in den homogenen, noch unberührten Film über.
Auf den ersten Blick würde man genau dies erwarten. Nicht aber auf den Zweiten! Schließlich stellt der Übergang auf der rechten Seite des Wulstes eine konkave Oberfläche dar, was aufgrund der Oberflächenspannung einen negativen Laplace-Druck im Film zur Folge hat. Es müsste demnach Material aus dem Wulst, aber auch aus dem noch unberührten Film dorthin strömen, zumindest dann, wenn sich das Filmmaterial wie eine Newtonsche Flüssigkeit verhält. Die unweigerliche Schlussfolgerung ist, dass rechts vom Wulst eine Senke im Film sein müsste, im Widerspruch zur Beobachtung. Tatsächlich kann man diese Senke beobachten, wenn man die Bedingungen richtig wählt. Abb. 5b zeigt ein solches Randprofil mit Senke, man erkennt sogar eine Art gedämpfter Oszillation, so wie man sie nach genauerer Rechnung auch theoretisch erwartet [10].
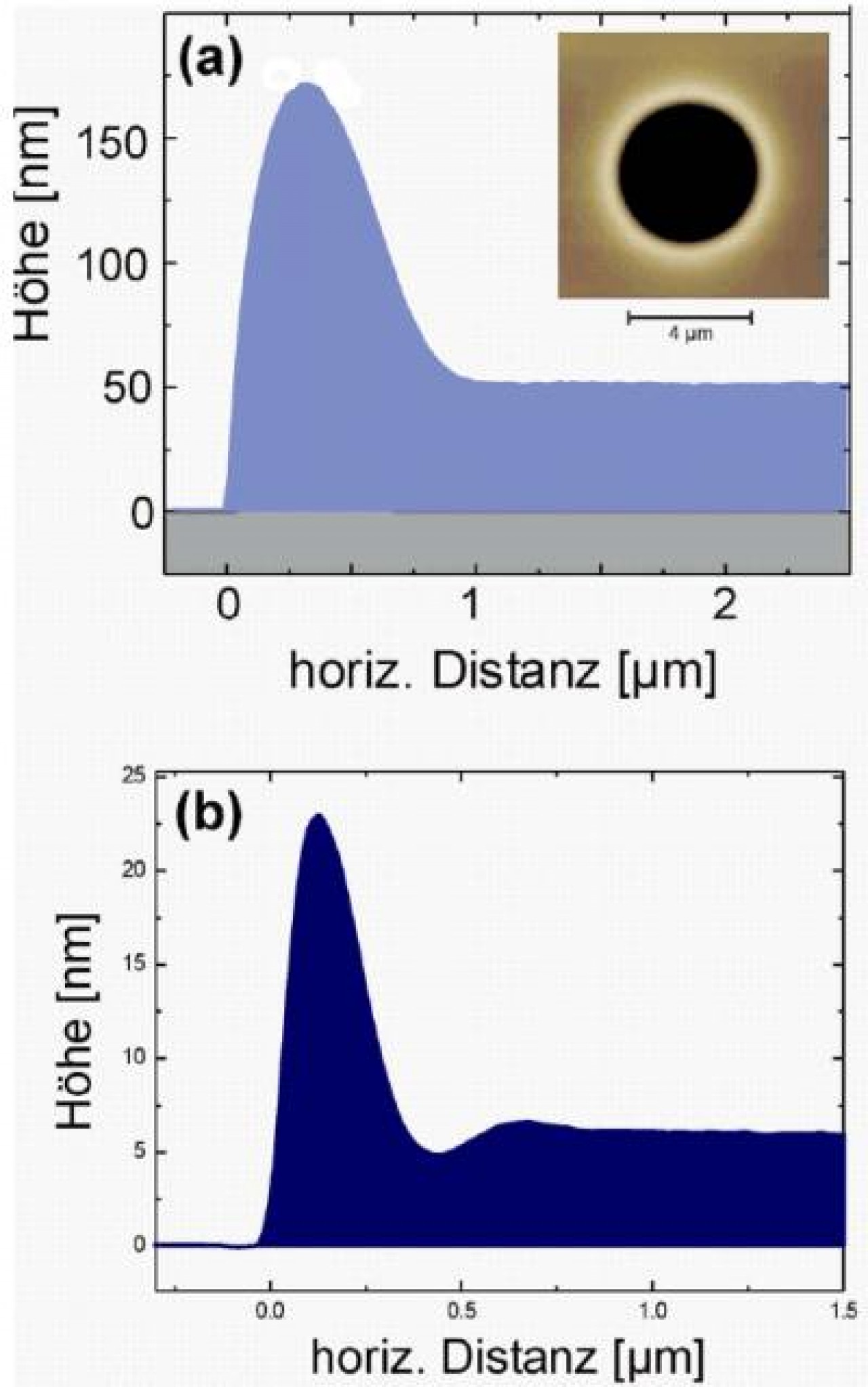
Abb. 5: Rasterkraftmikroskopische Aufnahmen der Lochrandwülste. a) Polystyrol, 18 kg/Mol. Der Einschub zeigt das Loch in Draufsicht. b) 2 kg/Mol. Man erkennt eine oszillatorische Struktur rechts vom Wulst.
Wiederum ist die Berücksichtigung der viskoelastischen Effekte im Material der Schlüssel zum Verständnis. Elastische Effekte können, dies zeigt die Theorie, die Senke zum Verschwinden bringen. In der Tat ist der wesentliche Unterschied zwischen den zu Abb. 5a und 5b gehörenden Proben das Molekulargewicht des Filmmaterials: 18 kg pro Mol für Abb. 5a, und 2 kg pro Mol für Abb. 5b. Bereits ein so kurzkettiges Material wie das für Abb. 5a verwendete ist offenbar elastisch genug, um die Senke zu verhindern. Wir sehen, dass die aufmerksame Beobachtung der Entnetzungsmorphologien uns wertvolle Informationen über die rheologischen Eigenschaften des Filmmaterials liefert. Letztere können, unter Zuhilfenahme meist analytischer Theorie, im Prinzip aus den gemessenen Profilen quantitativ ermittelt werden, und zwar, und das ist hier das Besondere, für Strukturen im Mikro- bis Nanometerbereich. Dass die Rheologie hier mitunter anders sein kann als auf makroskopischer Skala, hatten wir oben bereits gesehen.
Spätstadium
Wenden wir uns nun dem weiteren Verlauf des Entnetzungsprozesses zu. Wie entsteht aus einem Film mit einzelnen Löchern gewissermaßen das Gegenteil: einzelne Tropfen auf einem ansonsten trockenen Substrat (Abb. 1)? In Abb. 6 sieht man, wie die Randwülste zweier Löcher sich berühren und zu einem fast völlig geraden Wulst verschmelzen. Dieser repräsentiert eine zylindrische flüssige Oberfläche. Diese ist aber, wie man von der Rayleigh-Plateau-Instabilität des Wasserstrahls weiß, ihrerseits dynamisch instabil und zerfällt in eine Kette einzelner Tropfen. Auf diese Weise entsteht schließlich das häufig angetroffene Endstadium der Entnetzung: ein polygonales Netzwerk aus einzelnen Tropfenketten (vgl. Abb. 1b).

Abb. 6: Stoßen die Randwülste zweier Löcher aneinander, bilden sich zylindrische Kanäle aus (optische Mikroskopie in Reflexion).
Damit ist die Fülle der Phänomene aber noch nicht ausgelotet. Auch die Form der einzelnen Löcher kann ganz unterschiedlich ausfallen, je nach Material und Filmdicke. Abb. 7 zeigt zwei charakteristische Morphologien, wie man sie häufig beobachtet. Oben (a) erkennt man, wie der Randwulst selbst instabil geworden und in ein regelmäßiges Tropfenmuster aufgebrochen ist. Solche Mechanismen, die bei eher kurzkettigen Polymeren auftreten, modifizieren natürlich auch die Tropfenanordnung des Endstadiums. Unten (b) ist eine für langkettige Polymere charakteristische Morphologie zu sehen. Statt der Tropfen ergibt sich ein zickzackförmiger Rand, eingerissen durch die in diesem Material dominierenden elastischen Kräfte.

Abb. 7: Auch vor der Bildung zylindrischer Kanäle können die Lochränder im Polystyrolfilm instabil werden und charakteristische Strukturen entwickeln. a) zwölfzählige Rosette (65 k pro Mol, Dunkelfeldaufnahme). b) Aufgerissener Lochrand (600 kg pro Mol, Hellfeldaufnahme).
Ausblick
Auch aus den eben beschriebenen Strukturen kann man eine Menge über die dynamischen Eigenschaften des Polymeren auf kleinem und kleinstem Maßstab lernen. Hierzu muss im Wesentlichen die Theorie viskoelastischer dünner Filme und deren Instabilitäten noch weiterentwickelt werden. Daran wird zur Zeit in mehreren Gruppen intensiv gearbeitet. Ein visionäres Ziel ist hier, allein durch Analyse des Endstadiums alle wesentlichen Entnetzungsmechanismen sowie die rheologischen Eigenschaften des Films zu erschließen. Bis man allerdings die gesamte Information, die in den Entnetzungsmustern steckt, ausnutzen kann, werden wohl noch einige Jahre vergehen.
Ein anderer Ansatz besteht darin, die oben beschriebene Strukturbildungsneigung zu zähmen, um gezielt fluide Mikrostrukturen zu erzeugen. Dies kann z. B. dadurch geschehen, dass man die Substratoberfläche chemisch strukturiert, und so die entstehenden flüssigen Gebilde in geordnete Bahnen lenkt [11]. Neuerdings werden Möglichkeiten erforscht, diese durch elektrische Felder zu beeinflussen. Vielleicht wird man einmal in der Lage sein, flüssige Strukturen und andere weiche Materie auf mikroskopischer Skala so gezielt zu manipulieren, wie dies im Bereich der Elektronik bereits Gang und Gäbe ist.
Literatur
[1] K. Jacobs, S. Herminghaus, K. R. Mecke, Langmuir 14 (1998) 965.[2] S. Herminghaus et al., Science 282 (1998) 916.
[3] R. Seemann, S. Herminghaus, K. Jacobs, Phys. Rev. Lett. 86 (2001) 5534.
[4] S. Herminghaus, K. Jacobs, R. Seemann, Europ. Phys. J. E 5 (2001) 531.
[5] J. L. Keddie, R. A. L. Jones, R. A. Cory, Europhys. Lett. 27 (1994) 59.
[6] J. A. Forrest, K. Dalnoki-Veress, Adv. Coll. Int. Sci. 94 (2001) 167.
[7] W. Götze, Th. Voigtmann, Phys. Bl. 57 (2001) 41.
[8] R. Seemann, S. Herminghaus, K. Jacobs, J. Phys. Cond. Mat. 13 (2001) 4925.
[9] S. G. Croll, J. Appl. Polym. Sci. 23 (1979) 848.
[10] R. Seemann, S. Herminghaus, K. Jacobs, Phys. Rev. Lett. 87 (2001) 196101.
[11] H. Gau, S. Herminghaus, P. Lenz, R. Lipowsky, Science 283 (1999) 46.
Glossar
Dilatometrie: Messung der thermischen Ausdehnung. Hier wurde die Filmdicke optisch bestimmt und ihre Änderung bei Erwärmung registriert.
Eigenmoden: bei einer Saite sind die Eigenmoden die harmonischen Schwingungen, derer sie fähig ist (Grundton plus Obertöne). Etwas Analoges existiert in jedem räumlich begrenzten System, so auch in einem dünnen Film.
Elastischer Schermodul: die elastische Rückstellkraft, die ein Material einer Verscherung entgegensetzt.
Glastemperatur bzw. Glasübergang: die Temperatur, bei der ein glasiger (d.h. nichtkristallin fester) Stoff weich wird.
Gyrationsradius: typische Ausdehnung eines statistisch geknäuelten Polymermoleküls.
Laplace-Druck: der zusätzliche Druck, der unter einer gekrümmten Flüssigkeitsoberfläche herrscht. In einem Tropfen herrscht z. B. ein erhöhter Druck (= positiver Laplace-Druck), da die Oberflächenspannung versucht, den Tropfen zu verkleinern, d. h. zusammen zu drücken.
Modenkopplung: das bisher einzige (allerdings recht komplizierte) mathematisch geschlossene Konzept, das den Glasübergang befriedigend beschreibt.
Rayleigh-Plateau-Instabilität: die von der Oberflächenspannung getriebene, spontane Umwandlung eines flüssigen Zylinders in einzelne Tropfen. Drosselt man den Strahl aus einem Wasserhahn stark, so kommt er Boden des Waschbeckens in Form einzelner Tropfen an. Der zunächst zylindrische Strahl hatte genügend Zeit, beim Fall in einzelne Tropfen zu zerfallen. Er tut dies, weil die Kugelform (Tropfen) das günstigere Verhältnis von Volumen zu Oberfläche aufweist als der Zylinder (Strahl).
Verhakungslänge: diejenige Länge der Moleküle, oberhalb der sich die Polymerschmelze wie ein verhaktes Polymer verhält. Ein gutes Modell für ein verhaktes Polymer sind frisch gekochte lange Spaghetti: versucht man eines herauszuziehen, wollen alle anderen mit!

 Deutsche Version
Deutsche Version